2012年考研数学强化阶段重要题型攻略(一)
来源:中国研招信息网www.eduyz.net 作者:yzw 时间:2011-07-28 04:11:42
- 核心提示:
对于考研数学中的求数列极限来说,一般有以下几种主要方法:(1) 如果已知数列的通项表达式,可转化为函数极限进行计算;(2) 若数列用递推公式给出,一般考虑用单调有界必有极限进行分析;(3) 通过对数列的通项适当放大、缩小,然后利用夹逼准则来求极限;(4) 利用定积分定义求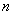 项和式或
项和式或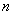 项积求极限。
项积求极限。
万学海文数学考研辅导专家们在此,主要为2012年的广大考生们来讨论一下使用夹逼准则求数列极限的方法。这种方法主要是应用在当某个数列迹象不是很好求解时,我们可以将该数列极限做适当的缩小和放大,得到另外两个极限式子比较好求,而这两个极限存在且相等,那么原来的极限就等于这两个极限的极限值.这种方法的困难之处就在于如何放缩,其要求是不仅放缩了之后的极限极限值存在,而且最终的极限值不能改变,而且还要放缩后的极限还是比较好求的,这也是考研考这一类题一个难点。
下面,我们来看一个用夹逼准则求数列极限的例题,来具体的体现以下夹逼准则求数列极限的方法。
例1 (I) 比较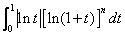 与
与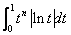 (
(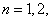 …)的大小,说明理由;
…)的大小,说明理由;
(II) 设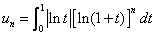 (
(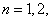 …)求极限.
…)求极限.
解:当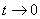 时,
时,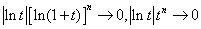 ,所以
,所以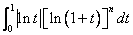 与
与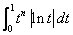
均为定积分,故
(I)当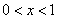 时
时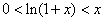 ,
,
故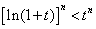 ,所以
,所以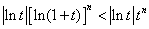 ,(
,(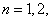 …)
…)
(II)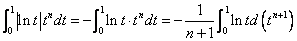
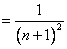
故由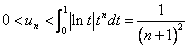 ,根据夹逼定理得
,根据夹逼定理得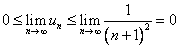
故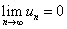 .
.
这是2010年数三的考题,其主要应用了夹逼准则求数列极限.数列极限是考研的重点,极限理论是高等数学的基础,极限的计算也是高等数学中最基本的运算,所以万学海文数学辅导老师们提醒2012年的考生这一部分掌握的程度直接关系到整个学科复习的效果,希望大家引起注意。


