名师指导:考研数学一 概率论与数理统计学习计划
来源:中国研究生招生网www.eduyz.net 作者:yzw 时间:2013-04-18 10:30:16
- 核心提示:
第三章 多维随机变量及其分布
对于二维随机变量,不仅应该理解二维随机变量联合分布函数的概念与性质,还要掌握二维离散型维随机变量的联合概率分布、边缘分布、条件分布和二维连续型随机变量的联合概率密度、边缘密度和条件密度。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2-3小时
|
二维随机变量的分布函数,二维离散型随机变量的概率分布和边缘分布,二维连续型随机变量的概率密度和边缘概率密度,例(77页)1-2,例(81页)1-2,习题(104页)2,3,5,7
|
1、理解多维随机变量的概念,理解多维随机变量分布的概念和性质,理解二维离散型随机变量的概率分布、边缘分布和条件分布,理解二维连续型随机变量的概率密度、边缘密度和条件密度,会求与二维随机变量相关事件的概率。
2、理解随机变量的独立性及不相关性的概念,掌握随机变量相互独立的条件。
3、掌握二维均匀分布,了解二维正态分布
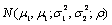 的概率密度,理解其中参数的概率意义。 的概率密度,理解其中参数的概率意义。 4、会求两个随机变量简单函数的分布,会求多个相互独立随机变量简单函数的分布。
|
|
2.5-3.5小时
|
二维离散型随机变量的条件分布,二维连续型随机变量的条件密度,相互独立的随机变量,例(84页)1-4,例(92页),习题(105页)8,9,11,12,13
|
|
|
2-3小时
|
两个随机变量的函数的分布,
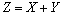 的分布, 的分布, 及 及 的分布,例(95页)1-4,习题(106页)17,19,24,26,27 的分布,例(95页)1-4,习题(106页)17,19,24,26,27 |
|
|
3小时
|
总结回顾,本章是的复习应从以下几个方面(1)联合密度与边缘密度,条件密度之间的关系与转化;(2)分布函数与概率密度的关系;(3)利用联合密度求概率;(4)独立性的判断与应用;(5)随机变量的简单函数的分布。习题(104页)6,10,14,16,20,23,25,28
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第四章 随机变量的数字特征
随机变量的数字特征是描述随机变量分布特征的数字,它们能够集中的刻画出随机变量取值规律的特点。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
数学期望的概念及性质,随机变量函数的数学期望,例(110页)1-12,习题(139页)3,5,8,9
|
1、理解随机变量数字特征(数学期望、方差、标准差、矩、协方差、相关系数)的概念,会运用数字特征的基本性质,并掌握常用分布的数字特征。
2、会求随机变量函数的数学期望。
|
|
2.5-3.5小时
|
方差、标准差的概念及性质,切比雪夫(Chebyshev)不等式,常见分布的数学期望和方差,例(122页)1-8,习题(140页)16,18,20,22,23
|
|
|
2.5-3.5小时
|
随机变量的协方差、相关系数的定义及性质,矩及协方差矩阵的定义及性质,例(132页)1-2,习题(141页)25,27,29,30
|
|
|
3小时
|
总结回顾,主要从以下几个方面复习本章内容(1)利用随机变量的概率分布求数学期望和方差;(2)利用常见分布的数字特征解决各种问题;(3)随机变量函数的数学期望;(4)数学期望和方差应用于数理统计问题;(5)协方差,相关系数等数字特征的计算;(6)相关系数为零(即不相关)与独立性的区别。习题(139页)6,7,13,19,21,24,28,31,33
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第五章 大数定律及中心极限定理
大数定律和中心极限定理都是随机变量序列的极限定理,它们是概率论中比较深入的理论结果。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
三个大数定律(切比雪夫(Chebyshev)大数定律,伯努利(Bernoulli)大数定律,辛钦(Khinchine)大数定律),三个中心极限定理(独立同分布的中心极限定理、李雅普诺夫(Liapunov)定理、棣莫佛-拉普拉斯(De Moivre-Laplace)定理),例(151页)1-3,习题(154页)1,4,7,8
|
1、了解切比雪夫不等式。
2、了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律(独立同分布随机变量序列的大数定律)。
3、了解棣莫弗-拉普拉斯定理(二项分布以正态分布为极限分布)和列维-林德伯格定理(独立同分布随机变量序列的中心极限定理)。
|
|
3小时
|
总结回顾,本章复习的重点应放在以下几个方面(1)利用切比雪夫不等式估计概率;(2)考查随机变量序列是否满足大数定律和中心极限定理的条件或结论;(3)利用中心极限定理解决应用中的近似计算问题。习题(154页)2,3,5,6,9
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
对于二维随机变量,不仅应该理解二维随机变量联合分布函数的概念与性质,还要掌握二维离散型维随机变量的联合概率分布、边缘分布、条件分布和二维连续型随机变量的联合概率密度、边缘密度和条件密度。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2-3小时
|
二维随机变量的分布函数,二维离散型随机变量的概率分布和边缘分布,二维连续型随机变量的概率密度和边缘概率密度,例(77页)1-2,例(81页)1-2,习题(104页)2,3,5,7
|
1、理解多维随机变量的概念,理解多维随机变量分布的概念和性质,理解二维离散型随机变量的概率分布、边缘分布和条件分布,理解二维连续型随机变量的概率密度、边缘密度和条件密度,会求与二维随机变量相关事件的概率。
2、理解随机变量的独立性及不相关性的概念,掌握随机变量相互独立的条件。
3、掌握二维均匀分布,了解二维正态分布
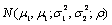 的概率密度,理解其中参数的概率意义。 的概率密度,理解其中参数的概率意义。 4、会求两个随机变量简单函数的分布,会求多个相互独立随机变量简单函数的分布。
|
|
2.5-3.5小时
|
二维离散型随机变量的条件分布,二维连续型随机变量的条件密度,相互独立的随机变量,例(84页)1-4,例(92页),习题(105页)8,9,11,12,13
|
|
|
2-3小时
|
两个随机变量的函数的分布,
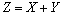 的分布, 的分布, 及 及 的分布,例(95页)1-4,习题(106页)17,19,24,26,27 的分布,例(95页)1-4,习题(106页)17,19,24,26,27 |
|
|
3小时
|
总结回顾,本章是的复习应从以下几个方面(1)联合密度与边缘密度,条件密度之间的关系与转化;(2)分布函数与概率密度的关系;(3)利用联合密度求概率;(4)独立性的判断与应用;(5)随机变量的简单函数的分布。习题(104页)6,10,14,16,20,23,25,28
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第四章 随机变量的数字特征
随机变量的数字特征是描述随机变量分布特征的数字,它们能够集中的刻画出随机变量取值规律的特点。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
数学期望的概念及性质,随机变量函数的数学期望,例(110页)1-12,习题(139页)3,5,8,9
|
1、理解随机变量数字特征(数学期望、方差、标准差、矩、协方差、相关系数)的概念,会运用数字特征的基本性质,并掌握常用分布的数字特征。
2、会求随机变量函数的数学期望。
|
|
2.5-3.5小时
|
方差、标准差的概念及性质,切比雪夫(Chebyshev)不等式,常见分布的数学期望和方差,例(122页)1-8,习题(140页)16,18,20,22,23
|
|
|
2.5-3.5小时
|
随机变量的协方差、相关系数的定义及性质,矩及协方差矩阵的定义及性质,例(132页)1-2,习题(141页)25,27,29,30
|
|
|
3小时
|
总结回顾,主要从以下几个方面复习本章内容(1)利用随机变量的概率分布求数学期望和方差;(2)利用常见分布的数字特征解决各种问题;(3)随机变量函数的数学期望;(4)数学期望和方差应用于数理统计问题;(5)协方差,相关系数等数字特征的计算;(6)相关系数为零(即不相关)与独立性的区别。习题(139页)6,7,13,19,21,24,28,31,33
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第五章 大数定律及中心极限定理
大数定律和中心极限定理都是随机变量序列的极限定理,它们是概率论中比较深入的理论结果。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
三个大数定律(切比雪夫(Chebyshev)大数定律,伯努利(Bernoulli)大数定律,辛钦(Khinchine)大数定律),三个中心极限定理(独立同分布的中心极限定理、李雅普诺夫(Liapunov)定理、棣莫佛-拉普拉斯(De Moivre-Laplace)定理),例(151页)1-3,习题(154页)1,4,7,8
|
1、了解切比雪夫不等式。
2、了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律(独立同分布随机变量序列的大数定律)。
3、了解棣莫弗-拉普拉斯定理(二项分布以正态分布为极限分布)和列维-林德伯格定理(独立同分布随机变量序列的中心极限定理)。
|
|
3小时
|
总结回顾,本章复习的重点应放在以下几个方面(1)利用切比雪夫不等式估计概率;(2)考查随机变量序列是否满足大数定律和中心极限定理的条件或结论;(3)利用中心极限定理解决应用中的近似计算问题。习题(154页)2,3,5,6,9
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第六章 样本及抽样分布
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
总体、个体、简单随机样本和统计量的定义,样本均值、样本方差和样本矩的定义,几个常用统计量的分布(
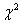 分布, 分布, 分布, 分布,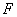 分布,正态总体的样本均值与样本方差的分布), 分布,正态总体的样本均值与样本方差的分布),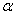 分位数的概念,习题(174页)1,4,9 分位数的概念,习题(174页)1,4,9 |
1、理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念。其中样本方差定义为:
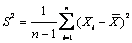 2、了解分布、分布和分布的概念及性质,了解上侧分位数的概念并会查表计算。
3、了解正态总体的常用抽样分布。
|
|
3小时
|
总结回顾,应重点复习数理统计的基本概念以及利用常见的分布及其相关理论求概率或数字特征。习题(175页)2,3,5,6,7,8
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第七章参数估计
参数估计问题分为点估计和区间估计。
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
点估计的概念,用矩估计法和最大似然估计法求点估计,估计量的评选标准(无偏性、有效性、相和性),例(176页)1-6,例(187页),例(189页)1-3,习题(207页)1,5,8,11
|
1、理解参数的点估计、估计量与估计值的概念。
2、掌握矩估计法(一阶、二阶矩)和最大似然估计法。
3、了解估计量的无偏性、有效性(最小方差性)和一致性(相和性)的概念,并会验证估计量的无偏性。
4、理解区间估计的概念,会求单个正态总体的均值和方差的置信区间,会求两个正态总体的均值差和方差比的置信区间。
|
|
2-3小时
|
区间估计的概念,单个正态总体均值、方差的置信区间,两个正态总体均值差、方差比的置信区间,例(196页)1-5,习题(210页)14,16,19,20
|
|
|
3小时
|
总结回顾,本章的复习重点应放在(1)求矩估计量和最大似然估计量;(2)验证估计量的无偏性及利用无偏性确定参数;(3)求正态总体参数的置信区间。习题(208页)3,7,9,12,13,15,18,21
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|
第八章假设检验
|
学习时间
|
复习知识点与对应习题
|
大纲要求
|
|
2.5-3.5小时
|
显著性检验的概念,假设检验的两类错误,假设检验的步骤,单个及两个正态总体的均值和方差的假设检验,例(213页)1-2,例(221页)1-3,例(227页)1-2,习题(263页)2,8,13,16
|
1、理解显著性检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产生的两类错误。
2、掌握单个及两个正态总体的均值和方差的假设检验。
|
|
3小时
|
总结回顾,本章应重点复习(1)假设检验中统计量的选取;(2)正态总体参数的检验过程;(3)假设检验中的两类错误;(3) 单个及两个正态总体的均值和方差的假设检验。习题(263页)3,4,9,10,14,15
|
|
|
2小时
|
本章测试题——检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格,继续进行下一章复习,如果不合格,总结自己的薄弱点要有针对性的对本章的内容进行复习或者到总部答疑。
|


